Zufallsvariablen und deren Verteilung
Aufgabe 1
-
A und B vereinbaren ein Würfelspiel: Zeigt der Würfel von A eine kleinere Augenzahl als der Würfel von B,
muss A an B 1.- Franken bezahlen und umgekehrt. Zeigen die beiden Würfel dieselbe Augenzahl, gewinnt keiner.
Bestimme die Verteilung der Zufallsgrösse X: Gewinn des Spielers A in einer Runde.
Aufgabe 2
- Du hast jetzt 9 Franken. Eine Münze wird geworfen: Erscheint „Kopf“, wird dein Vermögen verdreifacht, erscheint „Zahl“, wird dein Vermögen gedrittelt.
Welches Vermögen darfst du nach zweimaligem Werfen erwarten?
Aufgabe 3
- Ramona bietet Adrienne folgendes Spiel an: Für 2.- Franken Einsatz wird ein Würfel geworfen.
Zeigt er die „6“, so zahlt Ramona 10.- Franken, zeigt der Würfel die „1“, so zahlt Ramona 5.- Franken.
Ist das Spiel fair?
Aufgabe 4
- In amerikanischen Casinos findet das Würfelspiel „Chuck a luck“ grossen Anklang. Der Spieler darf auf eine der Zahlen 1, 2, 3, 4, 5, 6 setzen.
Dann werden drei Würfel geworfen. Erscheint seine Zahl ein-, zwei- oder dreimal, so erhält er das ein-, zwei- bzw. dreifache seines Einsatzes und
seinen Einsatz zurück. Andernfalls verliert er natürlich seinen Einsatz. Berechne den zu erwartenden Gewinn bei einem Einsatz von 10 $.
Aufgabe 5
- Ein Glücksspielapparat hat zwei Räder, die der Spieler durch Hebeldruck in Bewegung setzen kann. Auf jedem Rad sind vier Glocken, fünf Kirschen
und ein Apfel in regelmässigen Abständen abgebildet. Der Apparat zahlt für zwei Äpfel 10.- Franken, für zwei Glocken 2.- Franken und für zwei Kirschen 1.- Franken.
Der Einsatz beträgt 1.- Franken. Wer gewinnt hier?
Aufgabe 6
- Eine Haftpflichtversicherung stellt fest, dass 80 % der Versicherungsnehmer in den letzten drei Jahren keine Schadensmeldung abgegeben haben,
15 % eine, 3 % zwei und je 1 % drei bzw. vier Schadensmeldungen. Angenommen, die Verteilung bei den Schadensmeldungen bleibt gleich:
Mit wie vielen Schadensmeldungen pro Versicherungsnehmer wird die Versicherung in den nächsten drei Jahren rechnen müssen?
Aufgabe 7
- In einem Karton sind 6 Lämpchen, davon sind 3 defekt. Wie oft muss man im Mittel ziehen (ohne Zurücklegen) bis man
-
- ein brauchbares Lämpchen,
- zwei brauchbare Lämpchen gezogen hat?
Aufgabe 8
- Unter den 6 Glückszahlen einer Wochenziehung des Lottospiels „6 aus 49“ können k = 0, 1, 2, 3, 4, 5, 6 gerade (bzw. ungerade) Zahlen sein.
Bestimme die Verteilung der Zufallsgrösse X: Anzahl der geraden Glückszahlen einer Wochenziehung. Zeichne das zugehörige Histogramm.
Aufgabe 9
- Beim Lottospiel „ 3 aus 10“ werden 3 Glückszahlen gezogen. Betrachte die Zufallsgrösse X: Maximum der Glückszahlen. Bestimme ihre Verteilung.
Aufgabe 10
- Ein Würfel werde so lange geworfen, bis die Augenzahl 6 fällt. Betrachte die Zufallsgrösse X: Anzahl der Würfe, bis Augenzahl 6 fällt.
-
- Lege eine Tabelle an für k = 1, 2, 3, 4, 5, …, 15.
- Wie oft muss man würfeln, damit mit einer Wahrscheinlichkeit von mehr als 90 % mindestens eine 6 gefallen ist?
Aufgabe 11
- Für ein Schulfest soll ein Glücksrad gebaut werden, mit dem ein faires Spiel möglich ist.
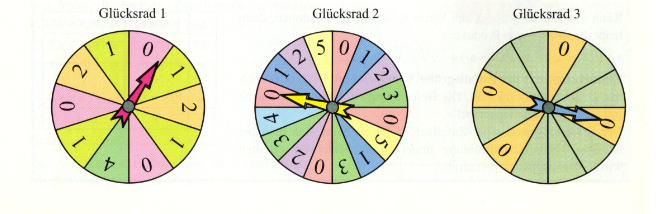
-
- Welcher Einsatz ist beim Glücksrad 1 bzw. 2 notwendig?
- Wie viele Sektoren müssen beim Glücksrad 3 die Aufschrift "1" (Fr.) bzw. "3" (Fr.) tragen, damit das Spiel bei einem Einsatz von 1 Fr. ein faires Spiel ist?